2025-04-02 오탈자 수정

Linear Models #

선형 모델은 numeric attribute들을 이용하여 수행된다. Regression, Classification을 수행하는 모델들을 먼저 학습한다.

• Regression
  • Uni variate case
  • Multivariate case
• Classification
  • Hard Threshold
  • Soft threshold: logistic regression

Uni variate Linear Regression #

데이터에 가장 fit한 $h_w$는 $h_w(x) = w_1x + w_0$을 통하여 찾을 수 있다. 이 때 weights들의 값을 찾기 위해서는 $L_2$ loss 값을 최소화 시켜야 한다. $$ Loss(h_w) = \sum_{j=1}^N L_2(y_j,h_w(x_j)) = \sum_{j=1}^N(y_j-h_w(x_j))^2= \sum_{j1}^N(y_j-(w_1x_j + w_0))^2 $$

$\sum_{j=1}^N(y_j-(w_1x_j + w_0))^2$를 최소화 하기 위해서 $w_0$와 $w_1$에 대해 모두 편미분을 해야 한다. $$ \begin{align*} &\frac{\partial}{\partial w_0}\sum_{j=1}^N (y_j-(w_1x_j + w_0)) = -2\sum_{j=1}^N(y_j-(w_1x_j + w_0)) = 0\newline &\rightarrow w_0 = (\sum y_j-w_1(\sum x_j))\newline\newline &\frac{\partial}{\partial w_1}\sum_{j=1}^N (y_j-(w_1x_j + w_0)) = -2\sum_{j=1}^N(y_j-(w_1x_j + w_0))x_j = 0\newline &\rightarrow w_1 = \frac{N(\sum x_j,y_j)-(\sum x_j)(\sum y_j)}{N(\sum x_j^2)-(\sum x_j)^2}\newline \end{align*} $$

$L_2$ loss function은 weight space에서 Convex함으로 local minima는 고려하지 않아도 된다.

linear model에 대해서 gradient descent를 적용하면 $w_i \leftarrow w_i - \alpha \frac{\partial}{\partial w_i} Loss(w)$를 만족한다. 여기서 $\alpha$는 learning rate이며 상수이다. $\alpha$값이 너무 작으면 정확하나 시간이 오래 걸린다는 단점이 있고 $\alpha$값이 너무 크면 비교적 빠르나 정확도가 떨어지게 된다. 따라서 leraning rate는 decay over time을 적용해 시간이 지날수록 값을 축소시킨다.

uni variate linear regression에는 아래와 같은 update rule이 사용된다.

• Batch gradient descent
• Stocahstic gradint descent

Batch gradietn descent #

• step마다 모든 트레이닝 데이터 사이클을 반복한다.
• $\alpha$값이 작기 때문에 convergence(수렴)을 보장한다.
• 속도가 느리다.

Stochastic gradient descent #

• single sample 또는 small set of samples에 대해서 step을 반복한다.
• convergence를 보장하지 않는다.
• 속도가 빠르다.

다시 돌아와서 $\frac{\partial}{\partial w_0}Loss(w)$를 이용하여 percentron learning rate를 표현할 수 있다. $$ w_0\leftarrow w_0 + \alpha (y-h_w(x))\newline w_1\leftarrow w_1 + \alpha (y-h_w(x))\times x $$

batch learning rule을 통해 모든 N개의 traing sample을 이용할 수 있다. $$ w_0\leftarrow w_0 + \alpha\sum_j^N (y_j-h_w(x_j))\newline w_1\leftarrow w_1 + \alpha\sum_j^N (y_j-h_w(x_j))\times x_j $$

Multivariate Linear Regression #

위의 Uni variate와 다르게 각 $x_j$가 $n+1$의 vector인 input attribute values라면 multivariate이다. $$ \begin{align*} &h_w(x_j) = w_0x_{j,0} + w_1x_{j,1} + \cdots + w_nx_{j,n} \newline &= \sum_i w_ix_{j,i} = w\cdot x_j = w^Tx_j\newline &where\ x_{j,0}=1\ \text{is a dummy input attribute(bias)} \end{align*} $$

best weight vector($w^*$) 는 loss를 minimize 시킨다. $$ w^* = \argmin_w \sum_j L_2(y_j,w^Tx_j) $$

Gradient descent로 weight를 구할 수 있다. $$ w_i \leftarrow w_i +\alpha \sum_j x_{j,i} (y_j-h_w(x_j)) $$

Uni variate linear regression과 마찬가지로 $w^*$는 행렬의 역산으로도 바로 구할 수 있다. $$ w^* = (X^TX)^{-1}X^Ty $$

관계가 없는 attribute들로 인한 오버피팅을 피하기 위해서는 regularization이 필요하다.

$$ \begin{align*} &Cost(h) = Loss(h) + \lambda Complexity(h)\newline &\hat{h}^* = \argmin_{h\in \mathcal{H}} Cost(h) \end{align*} $$

$\lambda$는 모델의 fit와 complexity 사이의 trade off를 제어한다. 최적의 $\lambda$를 찾기 위해서는 cross-validation이 필요하다. uni variate에서는 오버피팅을 상관하지 않아도 되지만 multivariate에서는 regulization을 이를 통해 방지해야 한다.

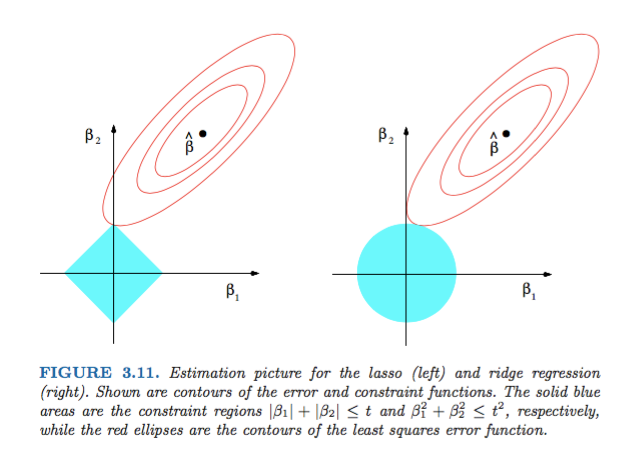
$Complexity(h_w) = R_q(w) = \sum_i|w_i|^q$이며 각각 $R_1$은 $L1\ norm$ $R_2$는 $L2\ norm$을 나타낸다. $R_1$은 weihts를 0으로 만들기 위해 sparse model을 만들게 되는 경향이 있다. 이를 feature selection효과라고 한다. 그렇기 떄문에 미분 불가능한 지점이 있고 이는 선형 해석이 안된다. 따라서 역행렬을 구하거나 유도해서 풀 수 없으므로 닫힌 해가 없고 직접 풀 수 없다.

$R_2$는 제곱을 하는 연산으로 인해 원형을 형성하며 모든 가중치를 조금씩 줄이는 방식이다. 닫힌 해가 존재하며 수학적으로 직접 풀 수 있다. 또한 feature selection은 이루어지지 않으므로 overfitting 방지에 효과적이다.

¹

L1 norm #

$$ ||x||_1 = \sum i = 1^n|x_i| $$

$L1-norm$은 각 원소의 절댓값의 합으로 표현된다. 따라서 $||x||_1 = 1$일 때 $(1,0)$ 또는 $(0,1)$이 되거나 $(\frac{1}{2}, \frac{1}{2})$가 된다. 이는 기하학적으로 좌우/상하 직각으로만 움직일 수 있다. 등거리로 표현하면 다이아몬드 형태가 나온다.

머신 러닝에서 L1 norm은 regularization에 사용되어 모델의 복자볻를 줄이고 sparse model을 만드는데 사용된다.

L2 norm #

$$ ||x||_2 = \sqrt{\sum i = 1^nx_i^n} = \sqrt{x^Tx} $$

L2 norm은 Euclidean norm이라고도 불리며 벡터의 크기를 나타낸다. 즉 벡터의 내적을 의미한다. 기하학적으로는 $||x||_2 = r$일 2차원에서는 원, 3차원에서는 구를 나타낸다.

해당 이미지에서의 등고선은 Loss funciton의 같은 값을 갖는 점들의 집합을 의미한다. 회색 도형은 각각 L1과 L2에 의해 제한된 공간 즉 제약 조건(C)를 의미한다.

Regularization #

$$ Cost(h) = Loss(h) + \lambda(Complexity(h) -c) $$

이는 손실을 최소화하되 복잡도는 일정 이하로 제한하라는 의미이다.

이미지에서의 동심원은 Loss(h)를 나타내며 중심에서 멀어질수록 손실이 큼을 나타낸다. 이 때 학습을 통해 중심에 최대한 가까운 점 즉 최소 Loss를 찾고 싶다.

회색 도형부는 정규화 영역으로 $Complexity(h) \le c$로 표현된다. 해당 조건은 어떤 도형 안에 모델 파라미터가 있어야 함을 나타낸다.

trainig을 통해 손실이 가장 낮으면서 제약 조건 안에 있는 점을 찾아야 한다. 즉 동심원으로 이루어진 등고선과 제약 영역의 점정르 찾아야 한다.

L1의 경우 다이아몬드 영역에서 꼭짓점과 등고선이 서로 만나 접점을 이룬다. 이 때 feature selection으로 인해 $w$는 sparse matrix가 될 가능성이 있다.

L2의 경우 원형 영역에서는 접점은 feature selection이 이루어지지 않아 Dense solution이 추론된다. 즉 $w_i$값은 작을 수 있어도 0은 아니게 된다.

라그랑주 승수법(Lagrangian) 제약 조건을 손실 함수 안으로 옮겨서 penalty로 처리하는것 따라서 Loss를 최소화하되 Complexity를 c라는 제약 조건 안에 두기 위해 Loss + (complexity -c)로 표현하며 제약 조건을 벗어나면 penalty가 커져 Cost값도 올라간다.

정리

1. Regulization은 Overfitting을 방지하기 위하여 사용한다.
2. L1 norm과 L2 norm 2가지를 사용할 수 있다.
3. $Cost(h) = Loss(h) + \lambda(Complexity-c)$
4. Cost를 최소화하기 위해서 Loss를 최소화, Complexity는 페널티로 부과, norm 영역 안에 있도록 강제한다.
5. c는 사용한 norm에 따라 다르며 L1 norm은 다이아몬드 형태, L2 norm은 원형 형태를 가진다.

Linear classifier with a hard threshold #

$\text{Linear descision boundary }= w\cdot x = 0\ (x_0 = 1\ \text{is a dummy input})$

$\text{Classification hypo} = h_w(x) =1\ \text{if}\ w\cdot x\le 0\ \text{and}\ 0\ \text{otherwise}$

즉 $w\cdot x \ge 0$이면 예측값은 1, 반대로 $w\cdot x < 0$이면 예측값은 0이 된다.

$$ h_w(x) = Threshold(w\cdot x) $$