Image Denoising #

Goal of the Denoising: Recover Noisy image to the original image

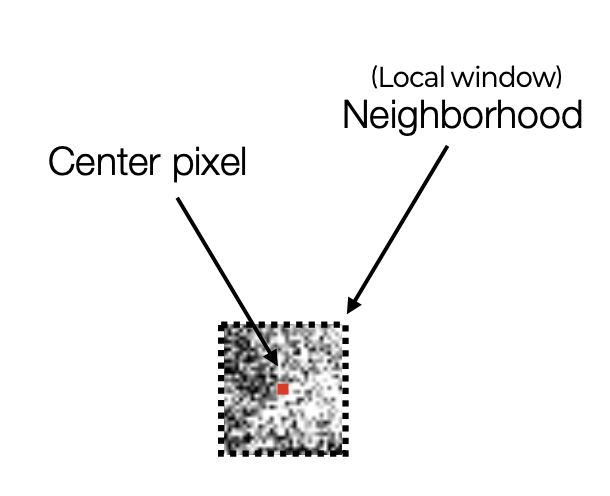
이를 위해 각픽셀을 이웃한 픽셀의 wegihted average로 변경해야 한다.

¹

Image

이미지는 배열로 나타낼 수 있다. Grayscale의 경우 숫자가 클수록 밝은 색이며 검정색에 가까울수록 그 값 또한 0에 가깝다.

Weighted Sum #

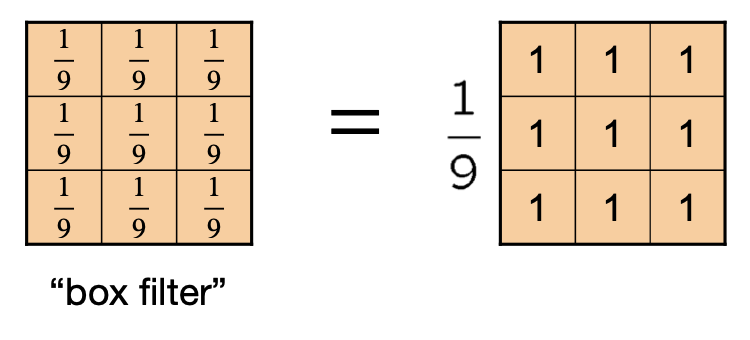
앞서 보았듯이 이미지 디노이징을 위해서는 해당 픽셀의 인접 픽셀들의 weighted average로 교체 하여야 한다. 이 떄 Weights를 filter kernel이라 한다. $3\times 3$ 인접 픽셀의 경우 아래와 같은 박스 필터를 가지게 된다.

²

해당 박스 필터를 이용해서 특정 픽셀의 인접 3x3 픽셀들에 모두 weight를 곱한 다음 평균을 낸 픽셀의 값을 해당 픽셀의 값으로 변경한다.

$$ \begin{bmatrix} 90\quad 90\quad 90\newline 90\quad 0\quad 90\newline 90\quad 90\quad 90\newline \end{bmatrix} \Longrightarrow Filter Kernel \Longrightarrow 80 $$

위와 같은 필터 커널로 weighted average를 구할 때 해당 픽셀 주위의 $3\times 3$ 범위에 픽셀이 없는 경우들이 있다. 예를 들어 Input의 가장자리 픽셀들의 경우는 박스 필터를 적용하지 못한다. 이럴 경우는 Padding을 추가하게 된다.

Padding은 Input iamge의 가장자리에 검정색 zero padding추가 하게 되며 $10\times 10$ 사이즈 이미지가 $11\times 11$ 이미지가 된다.

Padding의 종류

• zero padding
• circular repetition
• mirror edge pixels
• ground truth

Variance Filtering #

Impulse Filter $$ \begin{bmatrix} 0\quad 0\quad 0\newline 0\quad 1\quad 0\newline 0\quad 0\quad 0\newline \end{bmatrix} $$

Impulse Filter의 경우 원본 이미지와 똑같은 결과를 냄을 알 수 있다.

Translated Impulse

$$ \begin{bmatrix} 0\quad 0\quad 0\newline 0\quad 0\quad 1\newline 0\quad 0\quad 0\newline \end{bmatrix} $$

Impulse Filter와 유사하지만 원래 픽셀의 오른쪽 값만 살아 남는 것을 확인할 수 있다. 즉 원복 이미지에 비해 오른쪽으로 한칸 밀리는 이미지가 output으로 나온다. (Shifted left by 1pixel)

Box Filter

$$ \frac{1}{9} \begin{bmatrix} 1\quad 1\quad 1\newline 1\quad 1\quad 1\newline 1\quad 1\quad 1\newline \end{bmatrix} $$

Box Filter의 경우 인접 픽셀의 weight average를 반환하므로 Blurring이 됨을 확인할 수 있다. 그렇다면 아래의 필터는 어떠한 기능을 하는지 예측해보자.

Sharpening Filter $$ \begin{bmatrix} -\frac{1}{9} & -\frac{1}{9} & -\frac{1}{9} \newline\newline -\frac{1}{9} & \frac{17}{9} & -\frac{1}{9} \newline\newline -\frac{1}{9} & -\frac{1}{9} & -\frac{1}{9} \end{bmatrix} $$

위ㅌ의 필터는 아래와 같이 다시 분리할 수 있다.

$$ \begin{bmatrix} 0\quad 0\quad 0\newline 0\quad 2\quad 0\newline 0\quad 0\quad 0\newline \end{bmatrix} - \frac{1}{9} \begin{bmatrix} 1\quad 1\quad 1\newline 1\quad 1\quad 1\newline 1\quad 1\quad 1\newline \end{bmatrix} $$

먼저 첫번째 필터를 통해 원본 이미지의 각 픽셀의 값을 2배로 올린다. 이후 blur된 이미지의 값 즉 평균값을 빼줌으로 Sharpening의 효과를 얻을 수 있다.

Edge Detection #

Edge Detection을 위해서는 먼저 GrayScale로 이미지를 변경해야 한다.

Conversion to graysclae #

$$ I_{Gray}[y,x] = \frac{1}{3}\left(I_{rgb}[y,x,0]+I_{rgb}[y,x,1]+I_{rgb}[y,x,2]\right) $$ GrayScale 이미지는 2차원 평면에서 1차원의 값을 갖는다. 컬러 이미지의 경우 2차원 평면에서 RGB 3차원의 값을 갖는다. 원본 컬러 이미지에서 픽셀 3차원의 값들을 평균 낸 것이 grayscle 픽셀의 값이 된다.($I(x,y) = intensity\ at\ pixel(x,y)$)

Finding edges in image #

먼저 이미지의 Gradient는 아래와 같다. Gradient는 밝기의 x축과 y축을 따른 방향 변화율을 의미한다. $$ \nabla I = \left(\frac{\partial \mathbf{I}}{\partial x}, \frac{\partial \mathbf{I}}{\partial y}\right) \newline $$

실제 이미지는 이산값이므로 미분을 이용해 직접 계산할 수 없다. 하지만 근사적으로 두 픽셀 간 차이로 미분을 계산할 수 있다. 이를 Finite Difference Method라 한다. $$ \frac{\partial \mathbf{I}}{\partial x} \simeq \mathbf{I}(x,y) - \mathbf{I}(x-1,y) $$

Edge의 Strnegth는 아래와 같이 구할 수 있다. Euclidean Norm인 L2 Norm의 제곱으로 구할 수 있다. $$ E(x,y) = ||\nabla \mathbf{I}(x,y)||^2 = \left( \frac{\partial I}{\partial x}\right)^2 + \left(\frac{\partial I}{\partial y}\right)^2 $$ 즉 L2 Norm 제곱의 크기가 클 수록, 옆 또는 위 픽셀 간의 derivation값이 클 수록 에지일 가능성이 높음을 의미한다.

Edge의 orientation은 아래와 같다. Edge orientation은 어느 방향으로 edge가 변화하고 있는지 알려준다. 이는 기울기를 의미하며 graident의 y/x 비율로 각도를 계산한다. $$ \theta(x,y) = \angle \nabla \mathbf{I} = \arctan \frac{\partial\mathbf{I}/\partial y}{\partial \mathbf{I}/\partial x} \newline \tan \angle \nabla \mathbf{I} = \frac{\partial\mathbf{I}/\partial y}{\partial \mathbf{I}/\partial x} $$

Codes for Derivatives

Ix = np.zeros(I.shape) # empty numpy array
for y in range(I.shape[0]): # y축 의 범위
    for x in range(I.shape[1]): # x축의 범위
        if x-1 < 0: # 왼쪽 픽셀이 없는 경우
            Ix[y,x] = 0
        else: 
            Ix[y,x] = I[y,x] - i[y,x-1]
# numpy.ndarray.shape은 배열의 모양을 알려주는 튜플이다.
# 예를 들어 2x3인 배열인 경우 shape은 (2,3)이며 튜플은 []를 이용해 인덱스 접근이 가능하다.

x,y의 Derivates 값을 Filter로 보면 아래와 같다.

$$ d_x = \begin{bmatrix} 0 & 0 & 0 \newline -1 & 1 & 0 \newline 0 & 0 & 0 \end{bmatrix} $$ $$ d_y = \begin{bmatrix} 0 & 0 & 0 \newline 0 & 1 & 0 \newline 0 & -1 & 0 \end{bmatrix} $$ $$ \frac{\partial \mathbf{i}}{\partial x} \simeq \mathbf{I}(x,y) - \mathbf{I}(x-1,y) $$

Diffusion is Generating image by denoising

Neighborhood filtering은 아주 강력한 아이디어이며 CNN에서도 neighbor filtering이라는 기반 위에서 머신 러닝 시스템이 있는 형태이다. 즉 Filtering을 통해 32x32 매트릭스를 벡터로 표현할 수 있다.

Filtering #

필터링은 원하지 않는 소스는 제거하고 오직 작업과 관련된 정보만을 남기는 것을 의미한다.

$$ f[n,m] \rightarrow H(filter\ kernel) \rightarrow g[n,m] $$

Linear filtering #

$$ f[n,m] = \sum_{k=0}^{N-1}\sum_{l=0}^{M-1}h[n,m,k,l]g[k,l] $$

linear filtering의 필터는 2차원이 아닌 4차원이 중요하다. filter kernel h는 (n,m)위치에서 사용하는 필터가 (k,l) 위치의 입력 픽셀에 얼마나 영향을 주는지를 나타낸다. n, m은 출력 픽셀 위치이고 k, l은 입력 픽셀의 위치이다. 즉 출력 픽셀 위치에 따라 적용되는 필터 자체가 달라짐을 의미한다. 이러한 특성 때문에 linear filter는 translation invariance하다.

$$ f[10,10] = \sum_{k=0}^{N-1}\sum_{l=0}^{M-1}h[10,10,k,l]g[k,l] $$

Cross-correlation #

$$ g[m,n] = f\cdot h = \sum_{k=1}^N\sum_{l=1}^M f[m+k,n+l]h[k,l] $$

$f$를 이미지, $h$를 커널이라 하자. $g$는 output image이며 $f[m+k,n+l]$을 통해 m,n만큼 쉬프트 된 것을 알 수 있다. 또한 $h$는 zero padding으로 감싸 연산을 하도록 한다.

Convolution #

$$ g[m,n] = f\cdot h = \sum_{k=1}^N\sum_{l=1}^M f[m-k,n-l]h[k,l] $$

앞서 본 Correlation-cross와 연산이 매우 닮을을 확인할 수 있다. 이는 Coreelation-cross의 kernel이 flip되어 있는 형태를 의미한다.

Properties of the convolution

1. $h[n] \circ g[n] = g[n] \circ h[n]$
2. $h[n] \circ g[n] \circ f[n] = h[n] \circ ( g[n] \circ f[n]) = (h[n] \circ g[n]) \circ f[n]$
3. $h[n] \circ (f[n] \circ g[n]) = h[n] \circ f[n] + h[n] \circ g[n]$

Gaussian Kernel #

$$ G_\sigma = \frac{1}{2\pi \sigma^2} e ^{\displaystyle-\frac{(x^2+y^2)}{2\sigma^2}} $$

guassian kerenl을 이용해 합을 1로 만들 수 있다. 즉 normalization이 된다. 또한 corner부분을 확실하게 갖오하여 준다. 그렇기에 Gaussian standard deviation의 경우 $\sigma$가 커질수록 blur 처리가 더욱 강하게 된다. 퍼뜨리는 정도를 높였기 때문에 blur가 된다.

Gaussian filter에 Gaussian Filter를 convolve한다면 이는 또 다른 가우시안 필터가 나오게 된다. $$ \sigma \circ \sigma = \sqrt{2}\sigma $$

따라서 이미지에 계속 Gaussian filter를 적용하게 되면 $\sigma$값이 큰 gaussian filter를 적용한 것과 동일하다. $$ I\circ (h\circ h\circ \cdots \circ h) = ((I\circ h) \circ h)\circ \cdots \circ h $$

또한 2D Blur Gaussian Filter의 경우 1D Guasian filter를 x축, y축으로 돌리는 것과 동일하다. rectangular filter가 $(n\times 1)\ and\ (1\times n)$개가 존재한다. 이로 인해 빠른 속도를 보장 받는다. 커널의 크기가 $n\times n$이 었을 때는 $\mathcal{O(n^2)}$이지만 1차원 필터를 사용하면 $\mathcal{O(n)}$이 된다.